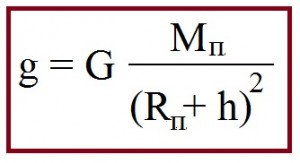16 листопада 2018 року
у Палаці Конгресу у Версалі відбулося засідання XXVI Генеральної конференції з заходів та ваг (ГКМВ). На голосування було поставлено резолюцію, що закріплює нові визначення чотирьох із семи базових одиниць Міжнародної системи одиниць СІ – кілограма, ампера, кельвіна та моля. Тепер систему СІ буде оновлено, і з неї зникне останній матеріальний еталон – еталон кілограма.

Тепер затверджено нове визначення кілограма, засноване на сталій Планка.
Нове визначення ампера буде з чисельним значенням електричного заряду.
Нове визначення кельвіна засноване на сталій Больцмана.
Моль буде визначений через зафіксовану сталу Авогадро.
Тепер всі одиниці будуть прив’язані до сталих, що не схильних до зносу.
Відмова від матеріальних зразків дозволяє різним державам створювати свої первинні еталони незалежно з інших країн. А від точних вимірювань часу, відстаней та мас сьогодні залежить безліч речей – від супутникової навігації, роботи мобільних телефонів до правильної роботи магазинних ваг.
Проект реформи був схвалений сьогодні, але набуде чинності у Всесвітній день метрології – 20 травня 2019 року.
ПОЯСНЕННЯ
У міжнародній системі одиниць вимірювання СІ (від французької Le System System d’Unites, SI) прийнято сім основних величин: довжина, маса, час, електричний струм, термодинамічна температура, кількість речовини та сила світла. Одиниці вимірювання дли них – основні одиниці СІ – метр, кілограм, секунда, ампер, кельвін, моль і кандела, відповідно. Для точного виміру базових величин вчені створюють еталони, оскільки вимір є порівняння чогось із еталоном.
Одиниця вимірювання довжини – метр – спочатку була прив’язана до довжини паризького меридіана, потім до довжини хвилі випромінювання атома криптона-86. Зараз метр визначається за допомогою сталої Планки: це відстань, яка проходить світло у вакуумі за 1/299 792 458 секунди.
Одиниця вимірювання времени – секунда – з 1967 року визначається як інтервал часу, що відповідає 9192631770 періодів випромінювання між двома надтонкими рівнями основного стану атома цезію-133.
Одиниця вимірювання сили світла – кандела – з 1979 року визначається як сила світла в даному напрямку від джерела, що випромінює монохроматичне випромінювання частоти 540 × 1012 герц, енергетична сила світла якого в цьому напрямку становить 1/683 вата на стерадіан (тут 683 — значення максимальної світлової ефективності, встановлене ГКМВ). Точне значення коефіцієнта максимальної світлової ефективності, що використовується разом з функцією, дає відношення сили світла до енергетичної сили світла монохроматичного випромінювання будь-якої довжини хвилі.
Майже всі одиниці теж поступово виявилися прив’язані до фундаментальних фізичних сталих (ФФС).
7 квітня 1795 року бюро мір і ваг прийняло за одиницю грама «абсолютну вагу об’єму чистої води, що дорівнює кубу [зі стороною] в соту частину метра, і за температури танення льоду». Для матеріалізації цієї маси спочатку створили еталон із платини.
Згідно з паризькою угодою 1875 року за одиницю вимірювання маси – кілограм – був прийнятий оригінальний циліндр діаметром і висотою 39,17 мм з платино-іридієвого сплаву (90% платини, 10% іридію), який зберігається в Міжнародному бюро мір та ваг (розташовано в Севрі біля Парижа). Сплав платини та іридію хімічно інертний, має високу твердість та зносостійкість, відносно малий коефіцієнт теплового розширення, велику густину та наділений парамагнітними властивостями.
Однак наприкінці минулого століття вчені виявили, що маса еталона кілограма змінювався приблизно на 0,3 мікрограми на рік, тобто на 30 мікрограмів за більш ніж 100 років. Це відбувається через випаровування атомів із поверхні циліндра. Це досить велике значення для сучасних вимог до точності. Кілограм є однією із семи основних одиниць СІ, і накопичені відхилення можуть стати причиною так званої технічної системної кризи. Саме тому наукова спільнота вирішила перевизначити кілограм через точно виміряну та фіксовану сталу Планку.
Установка, за допомогою якої можна реалізувати новий стандарт маси, називається ваги Кіббла.
 Ваги Кіббла використовувалися з середини 1970-х років для вимірювання величини сталої Планки. Співробітники Національного інституту стандартів США Пітер Мор та Баррі Тейлор у 1999 році запропонували зафіксувати величину сталої Планки та визначати масу за допомогою ваг Кіббла. Посмертно назване на честь винахідника Браяна Пітера Кіббла, це вдосконалені струмові ваги, в яких еталоном виступає вантаж, який врівноважує силу відштовхування між постійним магнітом та котушкою, якою пропускають струм. Таким чином, масу об’єкта можна знайти за рахунок рівності електричної та механічної сил.
Ваги Кіббла використовувалися з середини 1970-х років для вимірювання величини сталої Планки. Співробітники Національного інституту стандартів США Пітер Мор та Баррі Тейлор у 1999 році запропонували зафіксувати величину сталої Планки та визначати масу за допомогою ваг Кіббла. Посмертно назване на честь винахідника Браяна Пітера Кіббла, це вдосконалені струмові ваги, в яких еталоном виступає вантаж, який врівноважує силу відштовхування між постійним магнітом та котушкою, якою пропускають струм. Таким чином, масу об’єкта можна знайти за рахунок рівності електричної та механічної сил.
Одиниця вимірювання сили струму – ампер – затверджене в 1948 році, було засноване на вимірюванні сили, що діє на паралельні провідники зі струмом. Тепер нове визначення ампера засноване на численному значенні електричного заряду.
Одиниця вимірювання температури – кельвін – до сьогоднішнього дня визначалася як 1/273,16 термодинамічної температури потрійної точки води (це строго певні значення температури та тиску, при яких вода може одночасно і рівноважно існувати у твердому, рідкому та газоподібному станах). Це визначення створювало свої незручності, оскільки у воді завжди є домішки важких ізотопів водню та кисню, і вони можуть значно пересуває потрійну точку. Тому метрологам довелося створити окремий стандарт – Віденський стандарт усередненої океанської води. Її рецепт виглядає так: 0,00015576 моля дейтерію на моль звичайного водню. Крім того, для того, щоб визначати точні значення в інших діапазонах, ученим доводилося контролювати точки плавлення та кипіння кількох інших речовин. Нове визначення кельвіна засноване на сталій Больцмана.
Одиниця вимірювання кількості речовини – моль – була прив’язана до кількості атомів 0,012 кілограма стабільного вуглецю-12, тобто був пов’язаний з масою. Нове визначення моль буде визначено через зафіксовану сталу Авогадро.
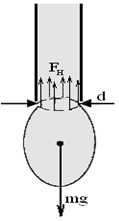
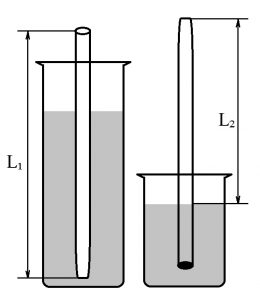
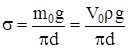 де V0 – об’єм однієї краплі, d – внутрішній диаметр трубки.
де V0 – об’єм однієї краплі, d – внутрішній диаметр трубки.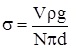
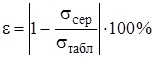 8. Зробити висновок, в якому зазначити: яку величину ви вимірювали; яким є результат вимірювання; у чому причина похибки вимірювання.
8. Зробити висновок, в якому зазначити: яку величину ви вимірювали; яким є результат вимірювання; у чому причина похибки вимірювання.

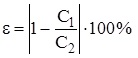


 Ваги Кіббла використовувалися з середини 1970-х років для вимірювання величини сталої Планки. Співробітники Національного інституту стандартів США Пітер Мор та Баррі Тейлор у 1999 році запропонували зафіксувати величину сталої Планки та визначати масу за допомогою ваг Кіббла. Посмертно назване на честь винахідника Браяна Пітера Кіббла, це вдосконалені струмові ваги, в яких еталоном виступає вантаж, який врівноважує силу відштовхування між постійним магнітом та котушкою, якою пропускають струм. Таким чином, масу об’єкта можна знайти за рахунок рівності електричної та механічної сил.
Ваги Кіббла використовувалися з середини 1970-х років для вимірювання величини сталої Планки. Співробітники Національного інституту стандартів США Пітер Мор та Баррі Тейлор у 1999 році запропонували зафіксувати величину сталої Планки та визначати масу за допомогою ваг Кіббла. Посмертно назване на честь винахідника Браяна Пітера Кіббла, це вдосконалені струмові ваги, в яких еталоном виступає вантаж, який врівноважує силу відштовхування між постійним магнітом та котушкою, якою пропускають струм. Таким чином, масу об’єкта можна знайти за рахунок рівності електричної та механічної сил.