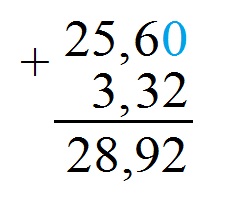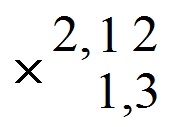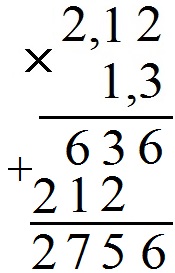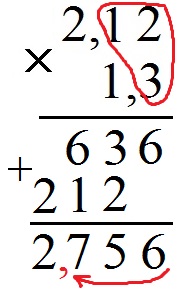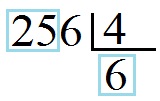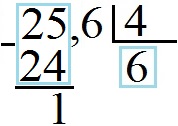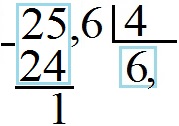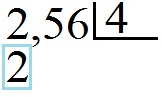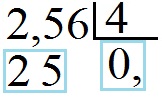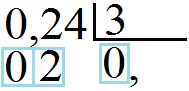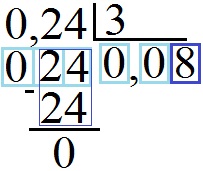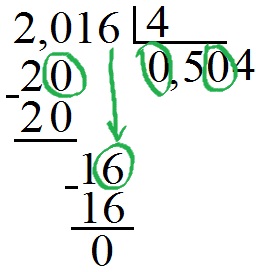При сложении и вычитании десятичных дробей важно запомнить, что целую часть мы складываем (вычитаем из) с целой частью, а дробную – с дробной.
При сложении и вычитании в “столбик” надо целую часть писать под целой, запятую – под запятой.

Примеры сложения
Пример 1: 25,6 + 3,32 = 28,92

Чтобы заполнить “пустое место” над 2, для удобства можно написать 0.
Пример 2:  4, 56 + 0,3 = 4,86

Примеры вычитания
Пример 1:  25,6 – 3,32 = 22,28

Многие ученики забывают, что после разряда десятых, в котором стоит 6, находится разряд сотых, в котором стоит 0, но его не пишут. При вычитании 0 следует писать, чтобы избежать ошибок.

Пример 2:  4, 56 – 0,37 = 4,19

При умножении десятичных дробей цифры распологаются друг под другом несмотря на запятую. Например, 2,12 × 1,3


Дальнейшее умножение “в столбик” производится так же как и с натуральными числами (на запятую не обращаем внимание):

Теперь осталось разобраться куда поставить запятую! Надо подсчитать сколько чисел стоит в множителях после запятой, а потом полученное количество отсчитать справа налево в произведении и поставить запятую.

2,12 × 1,3 = 2,756

Напомню, что в выражении a : b = c     a – делимое, b – делитель, c – частное

Деление числа на число выполняется при помощи таблицы, из-за особого вида которой данная процедура получила название деление «уголком».

Начнём с деления натурального числа на натуральное: 256 : 4, где 256 – делимое, а 4 – делитель. Таблица будет выглядеть так

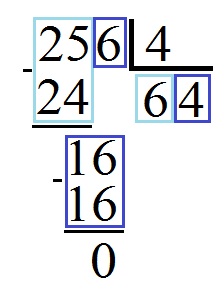
Рассмотрим подробнее.
При делении первых двух разрядов (25) на  четвёрку (4) получается  6  плюс еще какой-то остаток. Запишем 6 под чертой снизу от делителя.

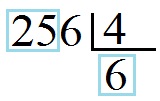
Умножаем на эту шестёрку  наш делитель (4) и записываем ответ 24 под первыми двумя разрядами делимого (25).

Выполняем вычитание «столбиком» и получаем единицу (1), к которой мы приписываем  шестерку  из следующего разряда делимого. В результате такого приписывания у нас получается число  16 .

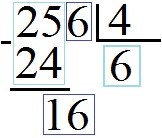
Мы делим его на наш делитель ( 4 ) и получаем  4 . Эту  четвёрку  пишем в строке ответа, под чертой снизу от делителя.

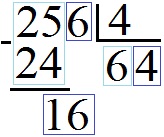
Умножаем делитель (4) на последнюю цифру ответа (4), приписываем результат 16  снизу к нашей таблице в последние два разряда делимого.

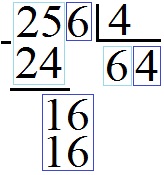
Вычитаем последнюю строку из предпоследней и получаем 0.

То есть 256 : 4 = 64

При делении десятичной дроби на натуральное число процесс тот же. Но только надо учитывать то, что теперь в делимом кроме целой части появляется дробная.

Разделим 25,6 : 4, где 2,56 – делимое, а 4 – делитель.
При делении целой части (25) на  четвёрку (4) получается  6  плюс еще какой-то остаток. Запишем 6 под чертой снизу от делителя. Умножаем на эту шестёрку наш делитель (4) и записываем ответ 24 под целой частью делимого (25). Выполняем вычитание «столбиком» и получаем единицу (1).

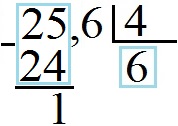
Всё как и в первом примере, разница только в том, что под чертой после 6 ставим запятую, потому что деление целой части закончилось.

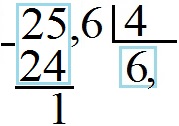
Дальше процесс деления повторяется точно как и в первом примере! В результате получим такую таблицу:

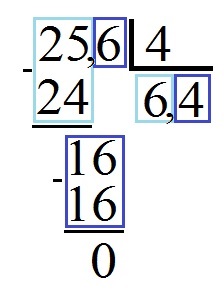
То есть 25, 6 : 4 = 6,4

Следующий пример это случай, когда целая часть делимого меньше делителя: 2,56 : 4, где 2,56 – делимое, 4 – делитель.

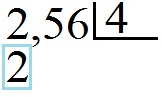
Видно, что двойки (2) мало для продолжения деления, нам нужна ещё одна цифра. Для этого сносим 5, но для этого придётся “заплатить нулём”. Запишем 0 под чертой снизу от делителя и поставим запятую, так как деление целой части закончено.

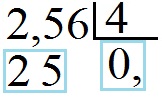
Дальше продолжаем деление по знакомой схеме и получим такую таблицу

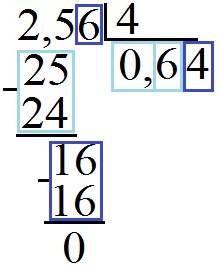
То есть 2,56 : 4 = 0,64

Усложним задачу. Пусть теперь целая часть десятичной дроби будет равна нулю.
0, 24 : 3, где 0,24 – делимое, 3 – делитель.

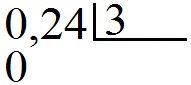
Начав деление мы увидели, что ноль меньше чем 3 и нам надо снести ещё одну цифру – 2. Но мы можем это сделать только “заплатив нулём”.  Запишем 0 под чертой снизу от делителя и снесём двойку. И поскольку деление целой части закончилось (мы начали использовать цифры после запятой), то после нуля под чертой мы ставим запятую.

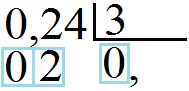
Но и двойки недостаточно для деления на 3. Нам надо снести ещё одну цифру, “заплатив нулём”. Мы сносим  четвёрку (4), под чертой снизу от делителя пишем ещё один 0.

Теперь при делении 24 на  тройку (3) получается  8. Запишем 8 под чертой рядом с нулём. Умножаем делитель (3) на последнюю цифру ответа (8), приписываем результат 24  снизу к нашей таблице в последние два разряда делимого. После вычитания в столбик получим 0.

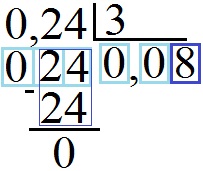
Таким образом, 0, 24 : 3 = 0,08

Для закрепления рассмотрим ещё один пример: 2,016 : 4 = 0,504

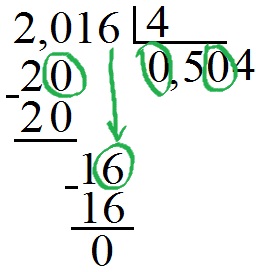
Поскольку целая часть делимого меньше делителя, то в целой части частного будет 0.  Так как 2 меньше 4, то сносим ещё одну цифру (0) и “платим нулём” в частном. 20 разделить на 4 будет 5, поэтому в частное пишим 5. После умножения 5 на 4 получим 20, и после вычитания в столбик получим 0. Сносим 1 – мало, сносим ещё одну цифру – 6, но “платим нулём” в частном. Очевидно, что 16 разделить на 4 будет 4. Поэтому в частное пишим 4. После умножения 4 на делитель (4) получим 20, и после вычитания в столбик получим 0.